Club Meeting: 23 Mar 2022
Report by: Strett Nicolson

Kevin De Freitas is a master at de-mystifying the secrets and mysteries of turning a great looking , well turned and perfectly working Singapore -Ball.

Kevin skipped through all the basic mounting, turning, finishing of a sphere and the creation of a sphere mounting jig (sphere chuck) and picked up his demo-lecture at the “How to” of marking out the points on the sphere for drilling the holes to house the spikes.

Again I must applaud Kevin for the clarity with which he purified the murky waters of the mathematics behind the location of the points for a perfect 6, 14, and 32 spiked Singapore Ball. If the challenges of the aforementioned SB ( Singapore Ball) are not challenging enough, he went on to illuminate the marking out process of a 12 and 20 point SB.

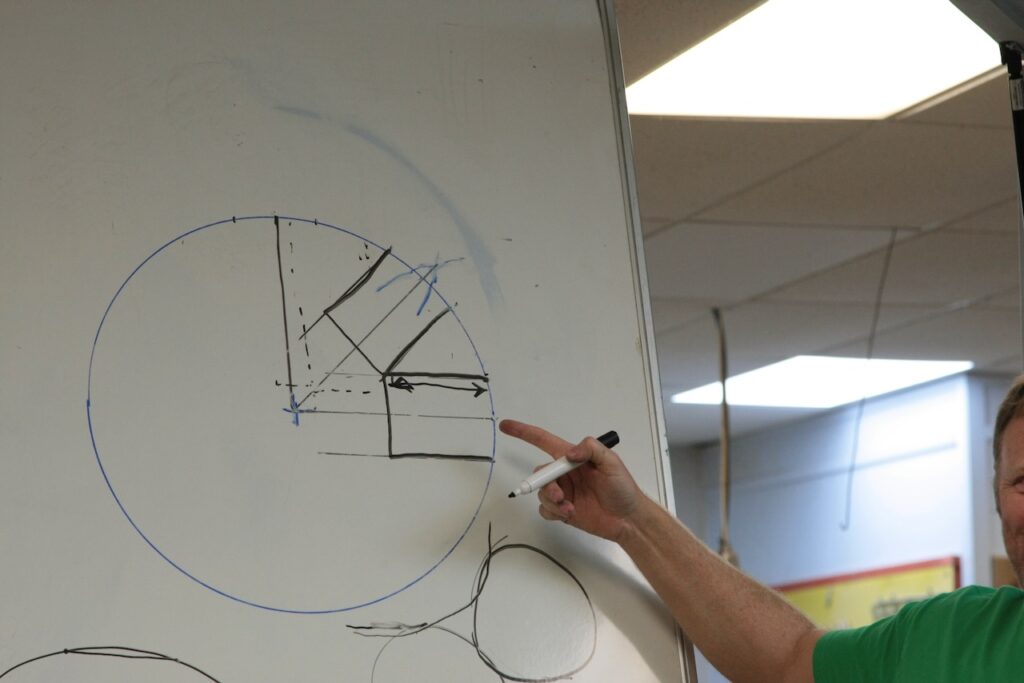
He provided various predetermined numerical factors that when multiplied by the diameter of the sphere determine the radius of a circle that would be used to draw circles and determine multiple point SB’s. ie, factor 0.3825 for a 14 point ball from 6 primary points or factor 0.5255 for a 32 point SB using a 12 primary points .

Quite simply a SB is created by using the points of a basic mathematical shape to mark the drilling points on the turned sphere. These drilled points will house the spikes. Kevin started his explanation using the triangle, I’ll explain this later. The various SBs mentioned above are spheres that are marked and drilled at the points of tetrahedron, octahedron, cube, ( although Kevin did not speak of an 8 pointed SB that would be the result of using a cube shape) icosahedron, dodecahedron. And/ or the use of the points of these mathematical shapes and then omitting certain points to create to achieve say a 20 or 15 point SB. The big question of course is how to determine the point on the sphere.

To create a 14 point SB, Kevin used the mathematical shape of the basic triangle. Firstly, the directional poles, north, south, east and west as well as the mid point between east and west on the equatorial circumference of a sphere are marked to create 6 basic points on your SB. To determine these 6 basic points see note below. To add 8 points for a 14 point SB one would simply scribe an ark, using a pair of compasses, from each point of a triangle created between a polar point and two adjacent points on the equator to find the middle of that triangle. Then working ones way around in each triangle of each hemisphere, one creates 4 points on each of the tropical lines of the sphere. so creating another 8 points. These points on the tropical line of each hemisphere together with the 6 original points make up the perfect 14 points to be drilled. Eureka! Mystery solved.

By mounting the sphere in his home made sphere chuck with a point perfectly centered a hole is drilled that is the exact diameter of the spike intended to be housed in the hole. Before moving the sphere to drill the next hole Kevin hollows out( about 1 mm) the hole drilled leaving about 2 mm depth at the mouth of the hole untouched. This will eventually be the stop that prevents the spike from falling out of the hole, once the spike is jammed or forced into the hole. So all 14 holes are drilled and hollowed ensuring that the holes drilled are deep enough to house the whole spike yet shallow enough for the core of the sphere not to become a lose piece of timber. Kevin only drilled and hollowed one hole as time did not permit any more turning than this.

The diameter of the spikes must be a fraction bigger in diameter than the holes drilled. A spike a fraction narrower will tend to fall out and a spike too thick will not be able to be fitted without damage to the sphere or spike and tend to stick. Kevin had a jig into which the point of the spike fitted to approximately half the length of the spike. Then by placing a sphere hole( hollowed out) perpendicularly above and onto the rear of the spike , with a sharp “bash” of the hand onto the top side of the sphere the spike is forced into the hole. ‘’Eureka’’ the mystery of fitting a spike into a hole the same diameter as the spike is demystified.

Some discussion followed regarding non mathematical determination of spike points on a sphere. Kevin believes that the points on basic mathematical shapes must be used to determine accurate and even placement of spikes points on in a sphere to create a well balanced SB. As a result of questions, Brian and others were challenged by Kevin to produce an SB with odd number of points to see if it works as efficiently as the mathematically determined fixed points. We wait to see if anyone rises to the challenge.

Note: The way to determine the first 6 basic points is to measure the diameter of the sphere ( at 3 or 4 different places and average the measurement) . Then multiply the diameter by 0.707 to set your pair of compasses to that length. Mark a starting point for later reference and use. Then along the equator line mark out with the length as determined above mark the 4 points on the equator line. These 4 points must be equidistant. Then using Pythagoras theorem ( the sum of the square on the hypotenuse is equal to the sum of the square on the other two sides) ( or simple doubling the measurement used on the equator) one determines the north and south pole points. Any of you marked points on the equator can be use to measure the North and South pole points. “Eureka’’ , you have your 6 basic points.

Mystery solved. Well done and thanks Kevin for a most interesting lecture.